فائزه حجتی | فروردین ۱۰, ۱۳۹۶ | 0 دیدگاه
جامعه آماری و نمونه آماری یکی از مباحث اولیه در تحقیق میباشد. پژوهشگران معمولاً کار خود را با توصیف اطلاعات شروع نموده (آمار توصیفی) و سعی میکنند آنچه را از بررسی گروه نمونه به دست آوردهاند، به گروههای مشابه بزرگتر یا جامعه آماری تعمیم دهند (امار استنباطی). بدین منظور در این مبحث با مفاهیم جامعه و نمونه آماری و و موضوعات مرتبط با آنها آشنا می شویم.
جامعه آماری
جامعه آماری عبارتست از مجموعه تمام افراد، گروهها، اشیاء و یا رویدادهایی که دارای یک یا چند ویژگی مشترک باشند. تعداد اعضای جامعه را حجم یا اندازه جامعه مینامند و با حرف بزرگ N نشان میدهند.
مثال: جامعه کارکنان شاغل در بانک تجارت شهر تهران
نمونه آماری
نمونه آماری گروه کوچکتری از جامعه است که طبق ضابطهای معین برای مشاهده و تجزیه و تحلیل انتخاب میشود و باید معرف جامعه باشد. نتایج نمونه ای را که معرف جامعه نباشد نمیتوان به جامعه تعمیم داد. تعداد اعضای نمونه را با حرف کوچک n نشان می دهند.
مثال: کارکنان شاغل در بانک تجارت منطقه ۵ شهر تهران
شکل ۱: جامعه آماری و نمونه آماری
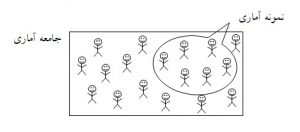
نمونهگیری به منظور گردآوری دادههای مورد نیاز درباره افراد جامعه و برآورد مقادیر جامعه به کمک مقادیر نمونه انجام میشود. نمونهگیری باعث صرفهجویی در هزینه و زمان است و کار تحقیق را ساده و امکانپذیر میسازد.
به طور کلی برای گردآوری اطلاعات دو روش وجود دارد:
الف) سرشماری: اگر محقق پژوهش خود را بر تمامی افراد جامعه اجرا کند روش او سرشماری خواهد بود. یعنی محقق باید تمامی افراد جامعه را تک تک مورد برسی و آزمون قرار دهد. هزینه، نیروی انسانی و مدت زمان لازم برای انجام شمارش کامل (برای گردآوری داده ها) به میزانی است که معمولاً اجرای آن توصیه نمی شود.
ب) نمونه گیری: نمونه گیری عبارت است از «انتخاب افراد گروه نمونه از میان اعضای یک جامعه ی تعریف شده ی آماری براساس اصول و قواعد خاص». در این شیوه دادهها از همه افراد جامعه گردآوری نمی شود.
نمونهگیری تصادفی یا احتمالی: در نمونهگیری تصادفی احتمال انتخاب شدن برای همه اعضای جامعه یکسان و معلوم است. هیچ عاملی جز شانس و تصادف در انتخاب شدن افراد نمونه از جامعه دخالت ندارد. نمونهگیری تصادفی انواع مختلفی دارد که عبارتند از: نمونهگیری تصادفی ساده، نمونهگیری منظم (سیستماتیک)، نمونهگیری طبقهای (یا نسبی) و نمونهگیری خوشهای (تک مرحلهای و چند مرحلهای). پژوهشگر میتواند بنا بر ویژگیهای جامعه آماری خود یکی از این روشها را برگزیند.
نمونهگیری غیر تصادفی یا غیر احتمالی: در نمونهگیری غیر تصادفی، احتمال انتخاب شدن برای همه اعضای جامعه نامعین و نامعلوم است. نمونه انتخاب شده به این روش معرف جامعه نیست و نمیتوان نتایج حاصل از آن را به جامعه تعمیم داد. نمونهگیری غیرتصادفی شامل نمونهگیری اتفاقی (یا در دسترس)، هدفمند (یا قضاوتی)، سهمیهای و شبکهای (یا گلوله برفی) میباشد.
جدول۱: روشهای نمونهگیری براساس قابلیت تعمیم
|
روشهای نمونهگیری تصادفی |
روشهای نمونهگیری غیر تصادفی |
|
۱. تصادفی ساده: همه افراد شانس برابر و مستقل برای انتخاب شدن دارند. |
۱. در دسترس: افراد فقط به دلیل سهولت، سادگی و در دسترس بودن انتخاب میشوند. |
|
۲. منظم (سیستماتیک): شکل اصلاح شده روش تصادفی ساده است. اما در این روش، نمونه با نظم خاصی بر اساس فهرستی که از قبل تنظیم شده انتخاب میشود. یعنی انتخاب افراد مستقل از یکدیگر نیست. |
۲. هدفمند (یا قضاوتی): نمونه براساس قضاوت شخصی و هدفهای مطالعه انتخاب میشود. |
|
۳. طبقهای (یا نسبی): در این روش، نمونه به گونهای انتخاب میشود که زیرگروههای آن به همان نسبتی که در جامعه وجود دارند، در نمونه نیز حضور داشته باشند. |
۳. سهمیهای: معادل نمونهگیری طبقهای است که محقق سعی میکند نسبت یا ویژگیهای جامعه در نمونه نیز وجود داشته باشد. |
|
۴. خوشهای: در این روش واحد نمونهگیری گروه یا خوشهای از افراد است. خوشهای چند مرحلهای: فهرست نمونهگیری دو بار یا بیش از دو بار تهیه میشود. |
۴. شبکهای (یا گلوله برفی): زمانی که شناخت اعضای یک جامعه دشوار باشد و نمونهها از یکدیگر شناخت داشته باشند، هر یک از افراد جامعه عضو دیگر را به پژوهشگر معرفی میکند. |
هر چه حجم نمونه بزرگتر باشد، میزان اشتباهات در نتیجهگیری کاهش مییابد و بر عکس. حجم نمونه ارتباط بسیار نزدیکی با آزمون فرضیه پوچ (صفر) دارد. بدین ترتیب که هر چه اندازه گروه نمونه بزرگتر باشد محقق با قاطعیت بیشتری فرض پوچ را که واقعاّ نادرست است رد میکند.

چنانچه نسبت ۰٫۰۵= n/N باشد، از رابطه بالا استفاده میکنیم، اما اگر این نسبت از ۰٫۰۵ بیشتر باشد، حجم نمونه را تعدیل کرده و از طریق فرمول زیر محاسبه میشود:
(n0= n/(1+n/N


محاسبه آنلاین حجم نمونه با فرمول کوکران (مشاهده)



برای مقایسه دو گروه از یک جامعه (مانند گروههای آزمایش و کنترل)، حجم نمونه مورد نیاز برای هر گروه از فرمول زیر به دست میآید:
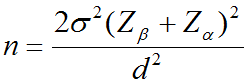

در رویکردهای کیفی برخی از متون پژوهشی تعداد واحدهای نمونه را برای گروههای همگون ۶ الی ۸ واحد و برای گروههای ناهمگون بین ۱۲ تا ۲۰ پیشنهاد میکنند. نمونهها اغلب بین ۴ تا ۴۰ نفر آگاهی دهنده را شامل میشود.
زمانی که نه از واریانس جامعه و نه از احتمال موفقیت یا عدم موفقیت متغیر اطلاع دارید و نمیتوان از فرمولهای آماری برای برآورد حجم نمونه استفاده کرد، از جدول مورگان استفاده میکنیم. این جدول توسط کرجسی و مورگان تهیه شده است.
|
حجم جامعه N |
حجم نمونه S |
حجم جامعه N |
حجم نمونه S |
حجم جامعه N |
حجم نمونه S |
حجم جامعه N |
حجم نمونه S |
حجم جامعه N |
حجم نمونه S |
| ۱۰ | ۱۰ | ۱۰۰ | ۸۰ | ۲۸۰ | ۱۶۲ | ۸۰۰ | ۲۶۰ | ۲۸۰۰ | ۳۳۸ |
| ۱۵ | ۱۴ | ۱۱۰ | ۸۶ | ۲۹۰ | ۱۶۵ | ۸۵۰ | ۲۶۵ | ۳۰۰۰ | ۳۴۱ |
| ۲۰ | ۱۹ | ۱۲۰ | ۹۲ | ۳۰۰ | ۱۶۹ | ۹۰۰ | ۲۶۹ | ۳۵۰۰ | ۳۴۶ |
| ۲۵ | ۲۴ | ۱۳۰ | ۹۷ | ۳۲۰ | ۱۷۵ | ۹۵۰ | ۲۷۴ | ۴۰۰۰ | ۳۵۱ |
| ۳۰ | ۲۸ | ۱۴۰ | ۱۰۳ | ۳۴۰ | ۱۸۱ | ۱۰۰۰ | ۲۷۸ | ۴۵۰۰ | ۳۵۱ |
| ۳۵ | ۳۲ | ۱۵۰ | ۱۰۶ | ۳۶۰ | ۱۸۶ | ۱۱۰۰ | ۲۸۵ | ۵۰۰۰ | ۳۵۷ |
| ۴۰ | ۳۶ | ۱۶۰ | ۱۱۳ | ۳۸۰ | ۱۸۱ | ۱۲۰۰ | ۲۹۱ | ۶۰۰۰ | ۳۶۱ |
| ۴۵ | ۴۰ | ۱۷۰ | ۱۱۸ | ۴۰۰ | ۱۹۶ | ۱۳۰۰ | ۲۹۷ | ۷۰۰۰ | ۳۶۴ |
| ۵۰ | ۴۴ | ۱۸۰ | ۱۲۳ | ۴۲۰ | ۲۰۱ | ۱۴۰۰ | ۳۰۲ | ۸۰۰۰ | ۳۶۷ |
| ۵۵ | ۴۸ | ۱۹۰ | ۱۲۷ | ۴۴۰ | ۲۰۵ | ۱۵۰۰ | ۳۰۶ | ۹۰۰۰ | ۳۶۸ |
| ۶۰ | ۵۲ | ۲۰۰ | ۱۳۲ | ۴۶۰ | ۲۱۰ | ۱۶۰۰ | ۳۱۰ | ۱۰۰۰۰ | ۳۷۳ |
| ۶۵ | ۵۶ | ۲۱۰ | ۱۳۶ | ۴۸۰ | ۲۱۴ | ۱۷۰۰ | ۳۱۳ | ۱۵۰۰۰ | ۳۷۵ |
| ۷۰ | ۵۹ | ۲۲۰ | ۱۴۰ | ۵۰۰ | ۲۱۷ | ۱۸۰۰ | ۳۱۷ | ۲۰۰۰۰ | ۳۷۷ |
| ۷۵ | ۶۳ | ۲۳۰ | ۱۴۴ | ۵۵۰ | ۲۲۵ | ۱۹۰۰ | ۳۲۰ | ۳۰۰۰۰ | ۳۷۹ |
| ۸۰ | ۶۶ | ۲۴۰ | ۱۴۸ | ۶۰۰ | ۲۳۴ | ۲۰۰۰ | ۳۲۲ | ۴۰۰۰۰ | ۳۸۰ |
| ۸۵ | ۷۰ | ۲۵۰ | ۱۵۲ | ۶۵۰ | ۲۴۲ | ۲۲۰۰ | ۳۲۷ | ۵۰۰۰۰ | ۳۸۱ |
| ۹۰ | ۷۳ | ۲۶۰ | ۱۵۵ | ۷۰۰ | ۲۴۸ | ۲۴۰۰ | ۳۳۱ | ۷۵۰۰۰ | ۳۸۲ |
| ۹۵ | ۷۶ | ۲۷۰ | ۱۵۹ | ۷۵۰ | ۲۵۶ | ۲۶۰۰ | ۳۳۵ | ۱۰۰۰۰۰ | ۳۸۴ |
همانطور که در جدول زیر مشاهده میشود به منظور فزایش سطح اطمینان و کاهش خطای نمونهگیری، محقق به حجم نمونه بالاتری نیاز دارد تا نمونه انتخابی معرف جامعه باشد.
|
حجم جامعه N |
حجم نمونهS (با سطح اطمینان ۹۵٪ و خطای نمونهگیری ۵٪) |
حجم نمونهS (با سطح اطمینان ۹۹٪ و خطای نمونهگیری ۱٪) |
| ۵۰ | ۴۴ | ۵۰ |
| ۱۰۰ | ۷۹ | ۹۹ |
| ۲۰۰ | ۱۳۲ | ۱۹۶ |
| ۵۰۰ | ۲۱۷ | ۴۷۶ |
| ۱۰۰۰ | ۲۷۸ | ۹۰۷ |
| ۲۰۰۰ | ۳۲۲ | ۱۶۶۱ |
| ۵۰۰۰ | ۳۵۷ | ۳۳۱۱ |
| ۱۰۰۰۰ | ۳۷۰ | ۴۹۵۰ |
| ۲۰۰۰۰ | ۳۷۷ | ۶۵۷۸ |
| ۵۰۰۰۰ | ۳۸۱ | ۸۱۹۵ |
| ۱۰۰۰۰۰ | ۳۸۳ | ۸۹۲۶ |
| ۱۰۰۰۰۰۰ | ۳۸۴ | ۹۷۰۶ |
۱۱- تعیین حجم نمونه برای رگرسیون چندگانه
از دیدگاه جیمز استیونس در تحلیل رگرسیون چندگانه با روش معمولی کمترین مجذورات استاندارد، باید به ازای هر متغیر پیشبین ۱۵ مورد در نظر گرفت (هومن، ۱۳۸۴).
قاعده سرانگشتی گرین (۱۹۹۱) برای تعیین حجم نمونه موردنیاز در در تحلیل رگرسیون به صورت زیر است:
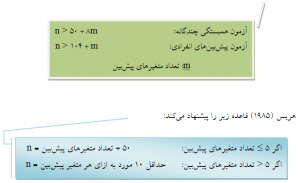
با اینحال در صورتی که شرایط اجازه میدهد، درصورتیکه به ازای هر متغیر پیشبین تقریباّ ۳۰ شرکت کننده وجود داشته باشد، محقق توان بهتری برای نمایان ساختن یک اندازه اثر کوچک خواهد داشت.
هنگامیکه متغیر وابسته دارای کجی و اندازه اثر کوچک باشد، خطای اندازهگیری زیاد و یا از رگرسیون گام به گام استفاده شود، حجم نمونه باید بزرگتر انتخاب شود.
تعیین حداقل حجم نمونه لازم قبل از گردآوری دادههای مربوط به مدلیابی معادلات ساختاری بسیار با اهمیت است. درحالیکه پژوهشگران با یکدیگر توافق دارند که در SEM برای دستیابی به توان آماری کافی و برآوردهای دقیق حجم نمونههای بزرگ لازم است، اما یک توافق کلی درباره روش مناسب برای تعیین تعیین حجم نمونه وجود ندارد. البته حجم نمونه به عواملی مانند نرمالیتی دادهها و روش برآوردی که پژوهشگر استفاده میکند، دارد. در رابطه با تعیین حجم نمونه در مدلیابی معادلات ساختاری دیدگاههای متفاوتی وجود دارند:
البته این قواعد با مشکلاتی مواجه میباشند. با توجه اینکه در این قواعد مدل مورد آزمون در نظر گرفته نشده است، درنتیجه ممکن است حجم نمونه کمتر یا بیشتر از حد لازم برآورد شود. عواملی مانند تعداد متغیرهای پنهان در مدل، تعداد شاخصها، شدت بارهای عاملی و ضرایب رگرسیون، نوع مدل و دادههای گمشده بر حجم نمونه تأثیر میگذارند. همچنین توان آماری نیز مهم است. معمولاً مدلهایی که در آن شاخصهای بیشتری برای هر عامل وجود دارد و بارهای عاملی بزرگتری دارند، در نمونههای بزرگ از احتمال همگرایی بیشتری برخوردار میباشند.
مدلیابی معادلات ساختاری (مشاهده)
تحلیل عاملی یکی از رویکردهای آماری با نمونه بزرگ است که باید تعداد آزمودنیها بیشتر از متغیرها باشد. نسبتهای مختلفی برای این منظور بیان شده است. یکی از آنها نسبت ۱۰ به ۱ است یعنی به ازای هر متغیر به ۱۰ نمونه نیاز داریم. نسبت قویتر در مورد تعیین حجم نمونه در تحلیل عاملی نسبت ۲۰ به ۱ یعنی حداقل ۲۰ نمونه به ازای هر متغیر است.
اشکال عمده این دستورالعملها این است که در تحلیل عاملی اکتشافی (EFA)، درباره نسبت بهینه تعداد موارد به تعداد شاخصها اتفاق نظر وجود ندارد. حجم نمونه به مدل عاملی جامعه (یا واقعی) بستگی دارد. بویژه اینکه هنگامیکه هر عامل دارای حداقل ۳ تا ۴ شاخص و متوسط اشتراکات در بین شاخصها ۰٫۷ و بالاتر باشد، تعداد موارد کمتری لازم است. یعنی نسبت ۱۰ به ۱ کافی است.
البته به یاد داشته باشید که در تحلیل عاملی حجم نمونه کمتر از ۱۰۰ غیرقابل دفاع است. برخی معتقدند که حداقل حجم نمونه در تحلیل عاملی ۲۰۰ نفر است.
۵۰ خیلی ناچیز (بسیار کم)
۱۰۰ ناچیز (کم)
۲۰۰ مناسب
۳۰۰ خوب
۵۰۰ خیلی خوب
۱۰۰۰ عالی
برای به دست آورن حجم نمونه در تحلیل عاملی تأییدی (CFA) از این نسبتها استفاده نمیشود. حجم نمونه در تحلیل عاملی تأییدی به تعداد پارامترها در کل مدل اندازهگیری بستگی دارد. این پارامترها عبارتند از: ضرایب الگو، واریانسهای خطا، کوواریانسهای خطا (برای خطاهای همبسته)، واریانسها و کوواریانسهای عاملها. بنابراین تحلیل عاملی تأییدی مستلزم تعداد برآوردهای بیشتری است و در نتیجه به حجم نمونه بزرگتری نیاز داریم تا نتایج از دقت و معقولیت لازم برخوردار باشند.
حجم نمونه در تحلیل عاملی تأییدی به نوع روش برآورد و ویژگیهای توزیع نمونه نیز بستگی دارد. اگر روش برآورد حداکثر درستنمائی (Maximum Likelihood) و توزیع نرمال باشد، به حجم نمونه کمتری نیاز است که در این صورت نسبت ۲۰ به ۱ توصیه میشود. به عنوان مثال در یک مدل تحلیل عاملی تأییدی با ۱۰ پارامتر ممکن است حجم نمونه ۲۰۰ نفر کافی باشد. اما در صورتیکه جهت برآورد مدل روشی به غیر از حداکثر درستنمائی به کار برده شود و توزیع متغیرها دارای انحراف جدی از توزیع نرمال باشند، باید حجم نمونه بسیار بزرگتر باشد.
تحلیل عاملی (مشاهده)
۱- حسن زاده، رمضان. (۱۳۸۳). روشهای تحقیق در علوم رفتاری. تهران: نشر ساوالان. چاپ سوم.
۲- دلاور، علی. (۱۳۸۸). مبانی نظری و عملی پژوهش در علوم انسانی و اجتماعی. تهران: انتشارات رشد. چاپ هفتم.
۳- سعدی پور، اسماعیل. (۱۳۹۳). روشهای تحقیق در روانشناسی و علوم تربیتی. تهران: نشر دوران. جلد اول.
۴- شوماخر، راندال ای و لومکس، ریچارد جی (۱۳۸۸). مقدمهای بر مدلسازی معادله ساختاری. مترجم: وحید قاسمی. تهران: انتشارات جامعه شناسان. چاپ اول. سال انتشار به زبان اصلی، ۲۰۰۴٫
۵- فراهانی، حجت الله و عریضی، حمیدرضا. (۱۳۸۸). روشهای پیشرفته پژوهش در علوم انسانی. اصفهان: انتشارات جهاد دانشگاهی. چاپ دوم.
۶- گنجی، کامران و حجتی، فائزه. (۱۳۹۴). سئوالهای آمار و روش تحقیق آزمون دکتری تخصصی مدیریت آموزشی. تهران: انتشارات رشد. چاپ اول.
۷- میرز، لاورنس اس، گامست، گلن و گارینو، ا. جی. (۱۳۹۱). پژوهش چندمتغیری کاربردی. (مترجمان: حسنپاشا شریفی، سیمین دخت رضاخانی، حمیدرضا حسنآبادی، بلال ایزانلو و مجتبی حبیبی). تهران: انتشارات رشد. چاپ دوم.
۸- هومن، حیدرعلی. (۱۳۸۸). مدلیابی معادلات ساختاری با استفاده از نرم افزار لیزرل. تهران: انتشارات سمت. چاپ سوم.
۹- هومن، حیدرعلی. (۱۳۹۳). شناخت روش علمی در علوم رفتاری. تهران: انتشارات سمت. چاپ ششم.
۱۰- Wilson Van Voorhis, Carmen R. and Morgan, Betsy L. (2007). Power and Rules of Thumb for Determining Sample Sizes. Tutorials in Quantitative Methods for Psychology, 3 (2), 43‐۵۰٫
۱۱- Kline, Rex. (2013). Exploratory and Confirmatory Factor analysis. retrieved from psychology.concordia.ca/fac/kline/library/k13b.pdf