میانجی “mediation”

فائزه حجتی | اردیبهشت ۱۲, ۱۳۹۶ | 0 دیدگاه

میانجی “mediation”

 

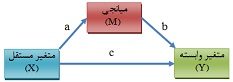
مدل میانجی چگونگی یا چرایی رابطه دو متغیر را توصیف می‌کند. در این مدل فرض بر این است که متغیر میانجی به عنوان رابط بین متغیر مستقل یا پیش‌بین و متغیر وابسته یا ملاک قرار می‌گیرد و رابطه متغیرهای مستقل و وابسته را تحت تاثیر قرار می‌دهد. با ورود متغیر میانجی به مدل، اثر غیرمستقیم مطرح می‌شود. بنابراین بایستی اثرات مستقیم، غیر مستقیم و اثر کل مورد بررسی قرار گیرند.

متغیر میانجی، متغیری است که برای رابطه بین متغیر پیش‌بین و ملاک دلیل ارائه می‌کند” (بارون و کنی، ۱۹۸۶، ص ۱۱۷۶).

ریشه و خاستگاه تکنیک میانجی “mediation” در حوزه علوم اجتماعی به ابداع شیوه تحلیل مسیر باز می‌گردد.

متغیر میانجی (M)، متغیری است که واجد شرایط زیر باشد:

1. متغیر مستقل باید همبستگی معناداری با متغیر میانجی داشته باشد.
2. متغیر میانجی باید همبستگی معناداری با متغیر وابسته داشته باشد.
3. هرگاه مسیرهای a و b کنترل شوند؛ رابطه بین متغیر مستقل و وابسته که پیشتر معنادار بوده؛ دیگر معنادار نباشد؛ ضمن اینکه هرگاه مسیر c صفر باشد؛ قوی‌ترین رابطه‌ی میانجی نمایان خواهد شد.

مثال

در یک تحقیق انتظار می‌رود که هر چه افراد رخدادهای مثبت بیشتری را در زندگی تجربه نمایند، شادی درونی بیشتری خواهند داشت. افزون بر این محقق پیش‌بینی می‌کند که قدرشناسی به عنوان یک میانجی سبب شادی درونی هرچه بیشتر در زندگی شود. به بیان دیگر، مقدار قابل توجهی از واریانس مشترک بین رخدادهای مثبت زندگی و شادی درونی به وسیله مسیر غیرمستقیم و با واسطه قدرشناسی تبیین می‌شود. یعنی این که اگر افراد در زندگی خویش وقایع و رخدادهای مثبت بیشتری را تجربه نمایند؛ سپاس‌گزارتر و قدرشناس‌تر بوده و در نتیجه خود را شاد‌تر احساس می‌کنند.

معادلات رگرسیون برای مدل میانجی

در مطالعات اولیه بارون و کنی (۱۹۸۶) روش‌های علی را برای آزمون میانجی پیشنهاد کردند. اما در بیشتر تحقیقات اخیر از آزمون هایی استفاده شده است که براساس ضرایب حاصل از معادلات رگرسیون زیر به دست می‌آید:

(۱)‌‌             Y=i1+cX+e1
(۲)      Y=i2+c ́X+bM+e2
(۳)             M=i3+aX+e3

نمودار مسیر برای مدل میانجی

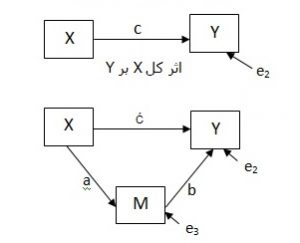
C: اثر کل  X بر Y

_Ć: اثر X بر Y با کنترل M

b: اثر متغیر میانجی بر Y

a: اثر X بر متغیر میانجی

i₁، i₂  و i₃: مقدار ثابت یا عرض از مبدأ هر معادله

e_1، e_{2 و} e₁: باقی‌مانده های مربوط به هر معادله

 

 

البته باید به این نکته توجه داشت که میانجی هنگامی رخ می‌دهد که با اضافه شدن متغیر میانجی، شدت رابطه اصلی بین متغیرهای پیش‌بین (X) و ملاک (Y) کاهش پیدا کند.

 

آزمون Z سوبل (Sobel Z) برای محاسبه میانجی

میانجی هنگامی رخ می‌دهد که با اضافه شدن متغیر میانجی، شدت رابطه اصلی بین متغیرهای پیش‌بین (X) و ملاک (Y) کاهش پیدا کند. سوبل در سال ۱۹۸۲ مقاله‌ای منتشر کرد که در آن یک آزمون آماری به منظور بررسی معناداری اندازه کاهش ارائه نمود. آزمون پیشنهادی سوبل در واقع آزمون معناداری اثر غیرمستقیم ab نیز نامیده شده است. زیرا نقش میانجی از طریق اثر غیرمستقیم ab تعیین می‌شود. این آزمون شناخته شده‌ترین و پر کاربردترین روش است. بر اساس این آزمون می‌توانیم نتیجه گیری کنیم که آیا کاهش در اندازه اثر مستقیم متغیر X بر روی متغیر Y به آن اندازه بوده که بتوان آن را به لحاظ آماری معنادار در نظر گرفت!

a*b گرچه در برآورد میزان اثر غیرمستقیم کمک می‌کند، اما دارای خطای سوگیری است. همچنین در صورت استفاده از آزمون سوبل در داده‌های غیر نرمال می‌تواند منجر به برآوردهای سودار شود. بنابراین پیشنهاد می‌شود که پژوهشگران اثر غیرمستقیم را با استفاده از تکنیک بوت‌استرپینگ برآورد کنند که برای توزیع‌های کوچک و یا غیر نرمال مناسب است.

فرمول Z سوبل به صورت زیر است:

a: ضریب رگرسیون غیراستاندارد برای مسیر X به M

b: ضریب رگرسیون غیراستاندارد برای مسیر M به Y (در رگرسیون همزمان متغیرهای X و M به عنوان پیش‌بین‌های Y)

S_a: خطای معیار مسیر a

S_b: خطای معیار مسیر b

پس از محاسبه مقدار z باید به جدول مقادیر z در کتاب‌های آمار یا برنامه‌های کاربردی آنلاین که مقادیر z را به p-value تبدیل می‌کنند، مراجعه کرد.

گرچه این معادله را به روش دستی می‌توان محاسبه کرد. البته یک روش آنلاین نیز وجود دارد که می‌توانید با وارد کردن مقادیر به دست آمده از خروجی دو مدل رگرسیونی، مقدار عدد z سوبل را به دست آورید.