فائزه حجتی | اسفند ۲۰, ۱۳۹۵ | 7 دیدگاه
رگرسیون به پیش بینی مقدار یک متغیر وابسته از روی مقادیر یک یا چند متغیر مستقل اشاره میکند. در رگرسیون به جای متغیر وابسته از اصطلاحاتی مانند متغیر ملاک، نتیجه، برونداد و … و به جای متغیر مستقل از اصطلاحاتی مانند متغیر پیش بین، اثر، درونداد و … استفاده میشود. به عنوان مثال، پیش بینی نشاط افراد براساس میزان امید به آینده، تحصیلات و درآمد. به طور کلی، اهداف تحلیل رگرسیون عبارتند از:
پدیده رگرسیون تحت عنوان بازگشت به سوی میانگین نیز مطرح میشود. میزان همبستگی بین دو متغیر، مقدار اتفاق رگرسیون را تعیین میکند. رگرسیون به طرف میانگین زمانی اتفاق میافتد که همبستگی بین دو متغیر کامل نباشد. دقت و صحت پیش بینی به قوت همبستگی بستگی دارد. هر چه همبستگی بین متغیرها بالاتر باشد، به همان اندازه پیش بینی دقیق تر است.
اگر همبستگی کامل باشد (۱± = r)، پدیده رگرسیون اتفاق نمیافتد یا وجود ندارد، ولی پیش بینی کامل و با دقت تمام انجام میشود.
اگر همبستگی بین متغیرها صفر باشد (۰ = r)، رگرسیون به طرف میانگین به طور کامل اتفاق میافتد. اما در این حالت قدرت پیش بینی وجود ندارد (بهترین پیش بینی میانگین است).
اگر همبستگی بین متغیرها بین ۱- و ۱+ و کامل نباشد، پیش بینی ما برآورد خوبی است ولی کامل نیست. هر چه همبستگی بین متغیرها بالاتر باشد، به همان اندازه پیش بینی دقیق تر است.
اگر نمرات X و مقادیر پیش بینی شده متناظر با آن ها (Ŷها) را در محور مختصات دو بعدی ترسیم کنیم. از میان این نقاط خطی میگذرد که به آن خط رگرسیون برای پیش بینی نمرات Y از روی X میگویند.
هر چه همبستگی ضعیفتر باشد، پراکندگی نقاط مختصات بیشتر میشود. هر چه همبستگی قویتر باشد، نمرات به خط رگرسیون نزدیکتر میشوند (بازگشت به میانگین). بنابراین، مقدار خطا در پیش بینی کمتر و پیش بینی دقیقتر خواهد بود. اگر ۱=r باشد، همه نقاط روی خط رگرسیون میافتند.
برای پیش بینی Y از روی X لازم است از دو عامل اطلاع داشته باشیم: شیب خط (b) و عرض از مبدأ (a)
شیب خط (b)، میزان تغییر در Y به ازای هر واحد تغییر در X را نشان میدهد.
عرض از مبدأ (a) نقطهای است که در آن خط رگرسیون محور Yها را قطع میکند. یا به عبارتی مقدار Ŷ را به ازای ۰=X نشان میدهد.
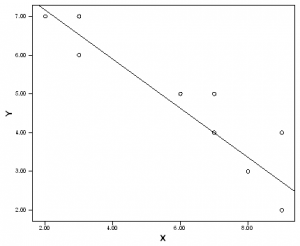
نمودار ۱: نمودار خط رگرسیون
معادله خط رگرسیون (رگرسیون خطی ساده) Y= a + bx
محاسبهی ضریب b:
(byx = rxy (Sy / Sx
rxy : ضریب همبستگی بین X و Y ؛ byx : ضریب یا شیب خط رگرسیون
Sx : انحراف استاندارد متغیر X؛ Sy : انحراف استاندارد متغیر Y
محاسبه ی a:
![]()
همخطی یعنی بین دو متغیر پیشبین همبستگی قوی وجود داشته باشد. همخطی چندگانه (multicollinearity) اصطلاحی برای توصیف وضعیتی در رگرسیون چندمتغیری است که در آن بین دو یا چند متغیر پیشبین همبستگی بالایی وجود داشته باشد. در این صورت ممکن است با وجود بالا بودن مقدار ضریب تعیین، مدل رگرسیون از اعتبار بالایی برخوردار نباشد. به عبارت دیگر با وجود آنکه مدل رگرسیون خوب بنظر میرسد، هیچ یک از متغیرهای مستقل اثر معنیداری در تبیین Y نداشته نباشند. علت آن این است که اگر همبستگی بین دو متغیر بالا باشد، احتمال دارد که این متغیرها دقیقاً واریانس مشابهی را در Y تبیین کنند.
فرض کنید X1 و X2 متغیرهای پیشبین و Y متغیر ملاک باشد. شکل ۱ انواع مختلف رابطه بین این سه متغیر و همخطی بین متغیرهای پیشبین را نشان می دهد.
شکل ۱: انواع مختلف همخطی در رگرسیون

بررسی همخطی در رگرسیون چند متغیری از طریق آمارههایی به نام تولرانس (tolerance) و عامل تورم واریانس (Variance Inflation Factor:VIF) اندازهگیری میشود. این شاخصها برای هر یک از متغیرهای پیشبین به طور جداگانه محاسبه میشود.
گرچه اصطلاحات رگرسیون چندگانه و رگرسیون چندمتغیره گاهی در ادبیات به جای یکدیگر به کار برده شدهاند، اما به دو نوع تحلیل متفاوت اشاره میکنند:
الف) رگرسیون چندگانه:برای پیش بینی یک متغیر ملاک از روی چند متغیر پیش بین از مدل رگرسیون چندگانه استفاده می شود. برای مثال پیش بینی عزت نفس دانش آموزان توسط پیشرفت تحصیلی و درجه محبوبیت آنان در میان همکلاسان.
ب) رگرسیون چندمتغیره: از این روش زمانی استفاده می شود که هدف، پیش بینی همزمان چند متغیر ملاک توسط چند متغیر پیش بین باشد. از رگرسیون چندمتغیره معمولاً تحت عنوان رگرسیون کانونی نیز نام برده میشود. به عنوان مثال، محققی علاقمند به تعیین عواملی است که بر سلامت گیاهان بنفشه آفریقایی تاثیر میگذارند. او دادههایی را در رابطه با متوسط ضخامت برگ، جرم گره ریشه و متوسط قطر شکوفه و همچنین مدت زمانی که در محفظه فعلی بوده است، جمع آوری میکند. سپس برای متغیرهای پیش بین عناصر متعددی در خاک، مقدار نور و آبی که بته دریافت میکند را نیز اندازه گیری میکند.
در رگرسیون چندمتغیره باید همبستگی بین متغیرهای ملاک حداقل در حد متوسط باشد و باقیمانده مدل باید از نرمالیتی چندمتغیره برخوردار باشند. اجرای این روش در نمونههای کوچک توصیه نمیشود.
برای ورود متغیرها در مدل رگرسیون، ۵ روش در دسترس پژوهشگران قرار دارد که بسته به هدف خود میتوانند یکی از آنها را استفاده نمایند. این روشها از قبل در داخل برنامههای کامپیوتری طرح ریزی شدهاند و پژوهشگران هنگام استفاده از این روش ها به برنامه کامپیوتری اجازه می دهند که به طور خودکار تحلیل را اجرا کند. این روش ها عبارتند از:
۱) روش همزمان (Enter Method): در این روش، تمام متغیرهای مستقل با هم وارد تحلیل میشوند.
۲) روش گام به گام (Method Stepwise): در روش گام به گام، متغیرها را یک به یک وارد مدل میکند. یعنی ابتدا متغیری که بالاترین ضریب همبستگی را با متغیر وابسته دارد، وارد تحلیل میشود. در این روش ترتیب ورود متغیرها در دست محقق نیست.
۳) روش حذف (Remove Method): با این روش میتوان متغیرهای بلوک را از مدل رگرسیونی حذف کرد. روش حذف مانند روش همزمان است؛ اما کاربرد چندانی در رگرسیون چند متغیره ندارد، چون تحلیل واریانس را انجام نمیدهد.
۴) روش پس رونده (Method Backward): ابتدا مانند روش همزمان، کلیه متغیرهای مستقل وارد مدل میشود، اما برخلاف روش همزمان به مرور متغیرهای کم اثرتر یکی پس از دیگری از معادله خارج میشوند تا مقدار به حداکثر برسد.
۵) روش پیش رونده (Method Forward): ابتدا همبستگی ساده بین هریک از متغیرهای مستقل را با متغیر وابسته محاسبه و سپس متغیر مستقلی که بیشترین همبستگی را با متغیر وابسته دارد، وارد تحلیل میکند.
در رگرسیون خطی به عنوان مثال میتوان گفت هر چه اضطراب امتحان کمتر باشد، پیشرفت تحصیلی دانش آموزان بیشتر است، یعنی با کاهش اضطراب امتحان، پیشرفت تحصیلی افزایش مییابد. اما در صورتی که نتوانیم رابطهی میان متغیرها را به شکل خطی تبیین کنیم، از رگرسیون انحنایی استفاده میشود. برای مثال، بین اضطراب و عملکرد تحصیلی رابطهای غیرخطی وجود دارد. کمی اضطراب هنگام امتحان به عنوان مثال ریاضی میتواند مفید باشد. اما اگر این اضطراب بیش از اندازه افزایش یابد، بر عملکرد دانشجو تأثیر منفی خواهد داشت. یعنی رابطه مثبت بین اضطراب کم و عملکرد تحصیلی، با افزایش میزان اضطراب به رابطهای منفی گرایش پیدا میکند. مثالی دیگر از این نوع رابطه، همبستگی بین سن و توانایی جسمی میباشد. تا سن معینی با افزایش سن، توانایی جسمی افراد افرایش مییابد ولی از آن پس با کاهش قدرت بدنی همراه است.
رگرسیون انحنایی شامل ۱۱ نوع رگرسیون غیرخطی است که در جدول زیر ارائه شدهاند و باید بهترین مدل رگرسیونی را که با دادهها برازش دارد، انتخاب کنیم.
جدول ۱: انواع مدلهای رگرسیون
|
مدل رگرسیون |
معادله رگرسیون |
|
رگرسیون خطی (Linear) |
Y = a + bX |
|
رگرسیون لگاریتمی (Logarithmic) |
(Y = a + (b lnX |
|
رگرسیون معکوس (Inverse) |
(Y = a + (b / X |
|
رگرسیون سهمی (Quadratic) |
(Y = a + (b1X) + (b2 X2 |
|
رگرسیون درجه ۳ (Cubic) |
(Y = a + (b1 X) + (b2 X2) + (b3 X3 |
|
رگرسیون توانی (Power) |
Y =aXb1 یا (lnY = lna + (b1 * lnX |
|
رگرسیون مرکب (Compound) |
(Y =a(b1X |
|
رگرسیون منحنی (s (S-curve |
Y=ea+b1/x |
| ( Y=1/(1/u+ab1X , مقدار حد بالا: u |
|
|
رگرسیون رشد (Growth) |
Y=ea+b1x |
|
رگرسیون نمایی (Exponential) |
Y=aeb1x |
|
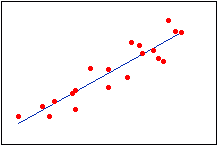
رگرسیون خطی |
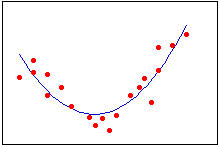
رگرسیون سهمی |
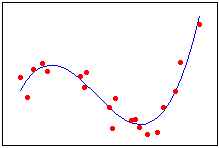
رگرسیون درجه ۳ |
 |
 |
 |
سلام و تشکر .مطالب بسیار خوب و آموزنده هستند .
با سلام و تشکر از زحمات شما،مطالب بسیار خوب ،جامع و آموزنده را ارایه کرده ایداز زحمات شما سپاسگزارم.
فائزه حجتی
از لطف جنابعالی سپاسگزارم
موفق باشید
سلام عزیزم. من همکلاسی قدیمی شما هستم. دنبال تعریف رگرسیون می گشتم که این مطلب را دیدم بی تعارف بگویم بهترین مبحثی که درباره رگرسیون مطالعه کردم. بسیار روان و ساده مبحث رگرسیون بیان شده. عالی بود. خیلی ممنون.
موفق باشید.
واقعا مرسی، علمتون روزافزون باد، تندرست و شاد باشید خانم حجتی، یک هفته س دنبال این مبحث بودم، اساتید هم که ماشاءالله اصصصصلا جواب نمیدن، مرسی مرسی
ممنون عالی بود برای دفاعم کلی به دردم خورد سپاس فراوان